Daily bit(e) of C++ | Advent of Code: Day 17
Daily bit(e) of C++ #350, Advent of Code using Modern C++: Day 17.
Welcome to day 17 of Advent of Code using Modern C++. Before you start reading, I highly encourage you to try to solve the two problems yourself: https://adventofcode.com/2023/day/17.
If you missed it, I have prepared a template repository for C++, with a development environment (through a devcontainer) with a bleeding edge version of the C++ toolchain: https://github.com/HappyCerberus/aoc-2023-cpp.
Today, we are transporting lava in temperamental crucibles.
Part one
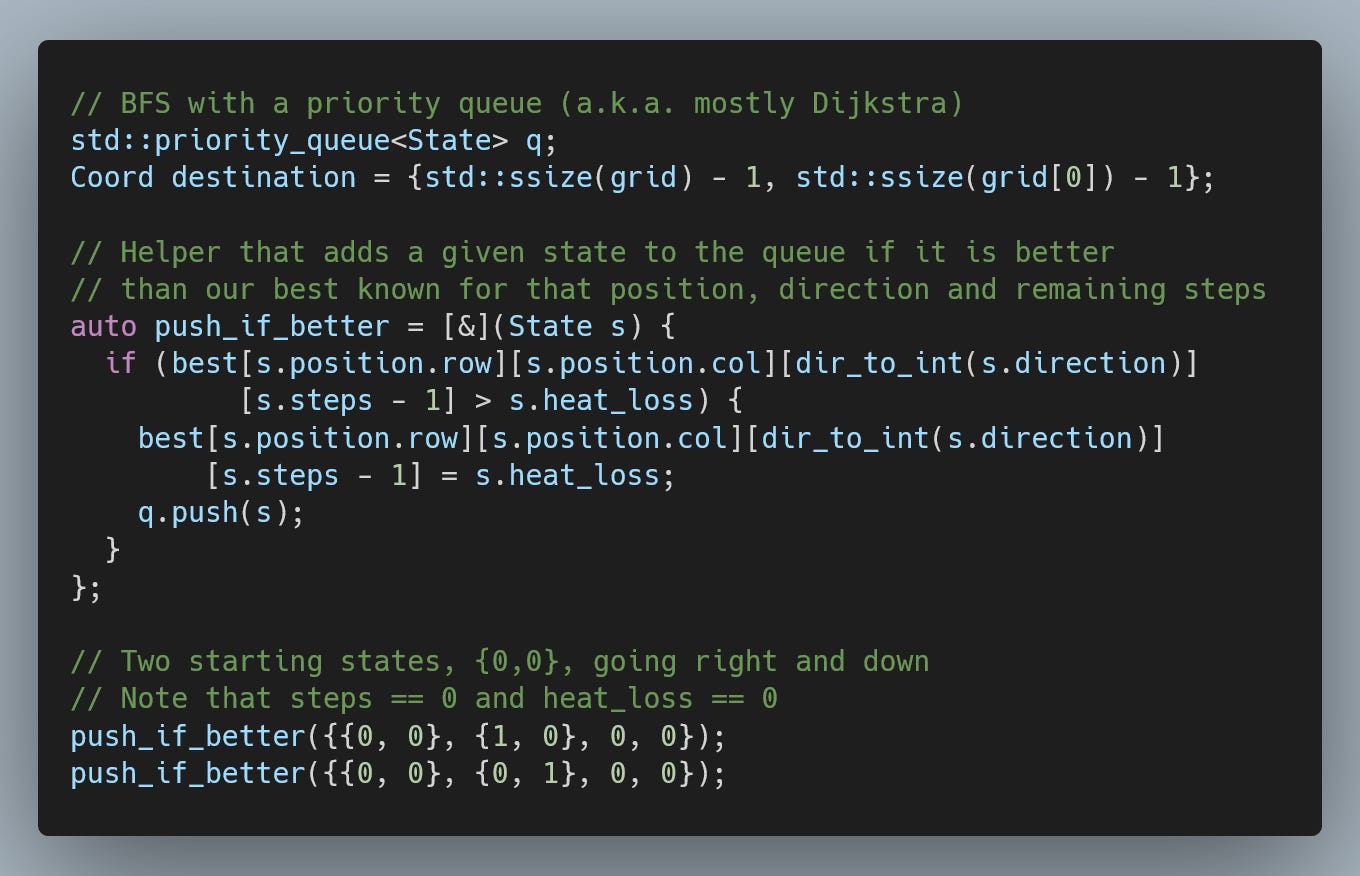
Since we are looking for the shortest path with weights (the heat loss), we need a Dijkstra-style search. The simplest way to achieve that is to slap a priority queue on a basic BFS and track the best distance for each space.
However, tracking the best distance for each space is where today’s problem becomes a bit complex since the direction from which we enter a space matters and on top of that, the number of steps we made in a straight line also matters.
I chose the brute-force approach of explicitly representing all the dimensions (i.e. rows*columns*(4 directions)*(3 possible remaining steps)).
This can be limited to rows*columns*2 by eagerly expanding the three allowed steps. Expanding the steps eagerly removes the need to track the state for steps at all, and because we can only expand left and right, the directions also collapse down to two (vertical and horizontal).
Either way, we first need to represent the state information.
Next, we need to parse out the lines from our text input. We will need to access the heat loss for a specific space and check whether we are out of bounds, which we can (as usual) wrap into small helpers.
We will also need logic for getting the direction to the right and left of our current direction.
This finally brings us to our BFS. First, we initialize our 4D array to track the minimum heat loss for each space.
We need to set up our priority queue with the initial state. As a reminder, the State implements the less-than operator in such a way as to keep the States with the lowest heat loss at the top of the queue.
Finally, we are left with the search itself.
Part two
For part two, we can reuse almost all of the above code. One change is that our 4D state array must now fit 10 potential steps (i.e. max_steps == 10). The second change is in our search logic because our constraints for going straight or turning have changed.
Conclusion
How did you do with today’s problems? Did you use the Dijkstra style approach, and if yes, did you represent the entire state or optimize with eager expansion?
Share your solutions and insights. Check out the repository with solutions and links to all articles: https://github.com/HappyCerberus/aoc-2023-cpp-solutions.