Daily bit(e) of C++ | Advent of Code: Day 25
Daily bit(e) of C++ #358, Advent of Code using Modern C++: Day 25.
Welcome to the final day of Advent of Code using Modern C++. Before you start reading, I highly encourage you to try to solve the two problems yourself: https://adventofcode.com/2023/day/25.
If you missed it, I have prepared a template repository for C++, with a development environment (through a devcontainer) with a bleeding edge version of the C++ toolchain: https://github.com/HappyCerberus/aoc-2023-cpp.
Today, we are analyzing the connectivity of a mess of components.
Part one
Today, we only have one part to deal with. However, it’s not a trivial one. What we are looking for is the k-edge-connectivity of a graph.
One of the approaches to determining the connectivity between two nodes is using the maximum flow between those two nodes. We are working with an unweighted, undirected graph; therefore, we can simplify. For this case, the maximum flow is simply the number of unique paths between the two nodes (paths that do not share edges).
We need a representation of our graph. I chose a neighbourhood map, which I filled in symmetrically, i.e., unlike the input, both edge directions are represented.
We need a path-finding routine. I chose BFS. Note that we need to return the list of nodes on the path to account for the uniqueness of paths.
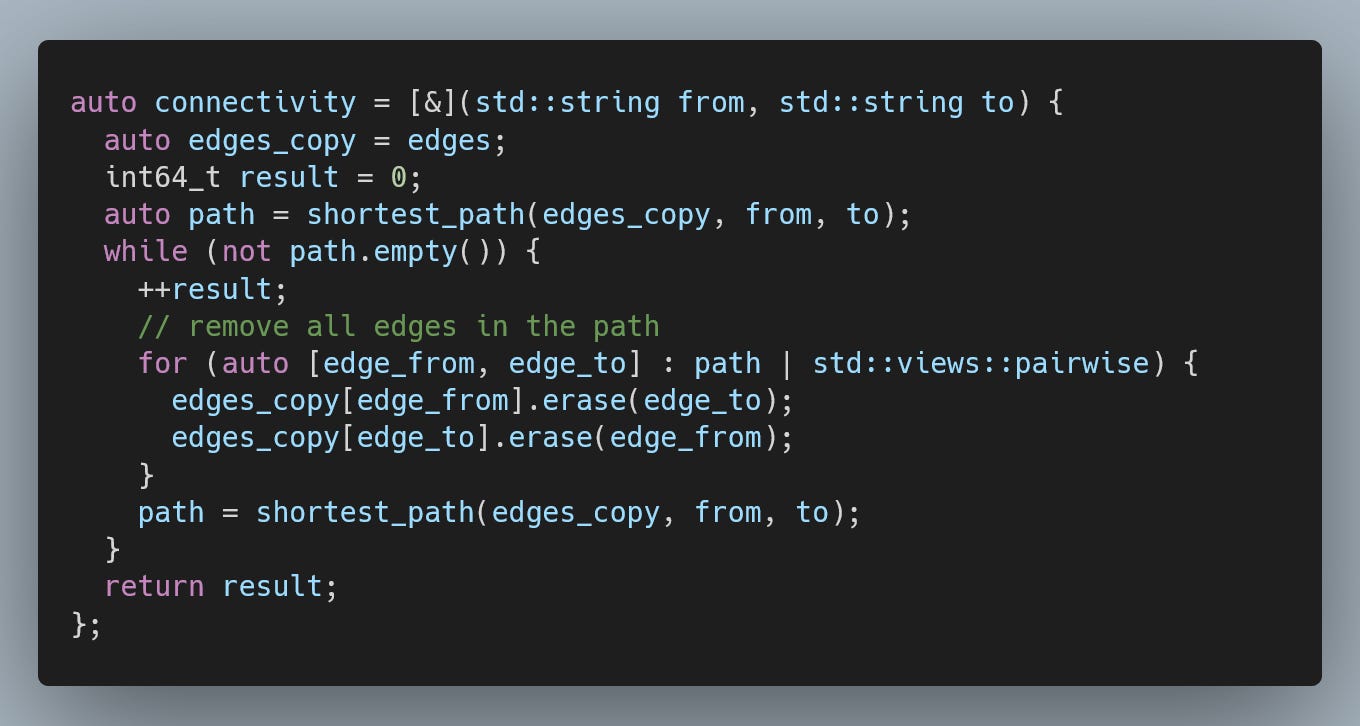
Now, for the connectivity computation. We repeatedly find a path and then remove all edges that are part of this path. This will give us the number of unique paths between the two nodes, i.e. their connectivity.
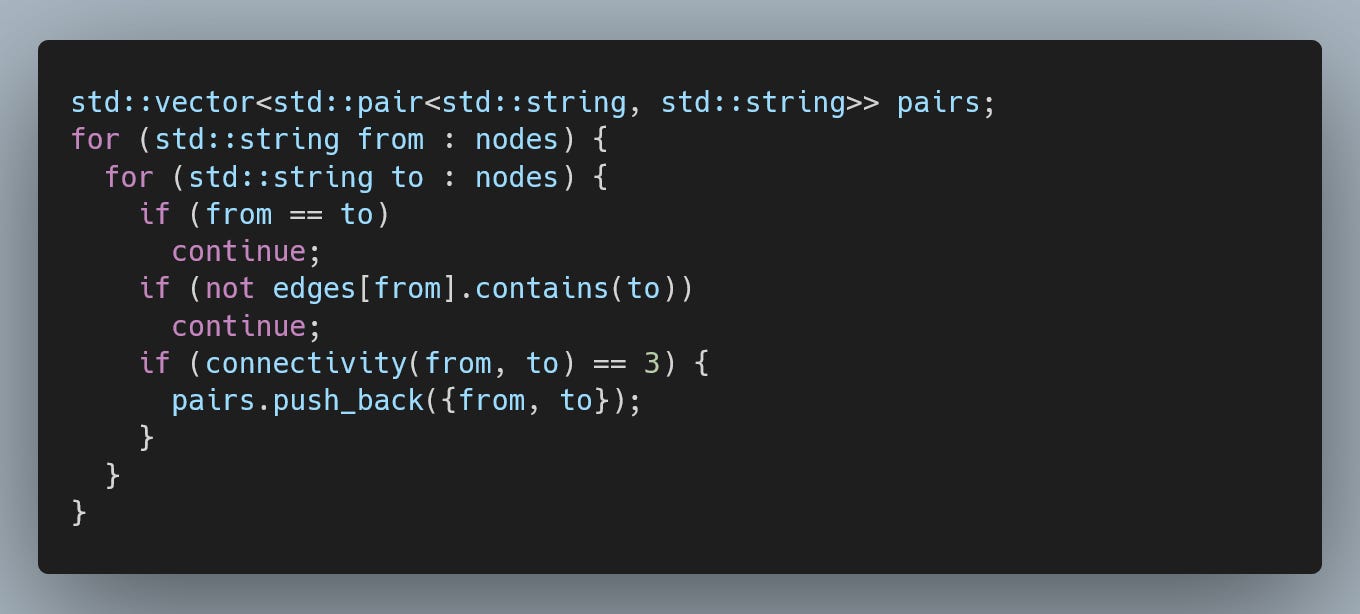
Which brings us to our main goal. Find the three edges that will disconnect the graph into two components. For this approach, this translates into iterating over all pairs of adjacent nodes and remembering the three pairs (six because of symmetry) that have only connectivity of three.
We can then remove the connecting edges and count the nodes in both components.
Conclusion
How did you do with today’s problems? This is the end of the AoC series, and normal Daily bit(e) programming will resume tomorrow. Did you enjoy this departure?
Share your solutions and insights. Check out the repository with solutions and links to all articles: https://github.com/HappyCerberus/aoc-2023-cpp-solutions.