Daily bit(e) of C++ | Advent of Code: Day 23
Daily bit(e) of C++ #356, Advent of Code using Modern C++: Day 23.
Welcome to day 23 of Advent of Code using Modern C++. Before you start reading, I highly encourage you to try to solve the two problems yourself: https://adventofcode.com/2023/day/23.
If you missed it, I have prepared a template repository for C++, with a development environment (through a devcontainer) with a bleeding edge version of the C++ toolchain: https://github.com/HappyCerberus/aoc-2023-cpp.
Today, we are going on a scenic stroll.
Part one
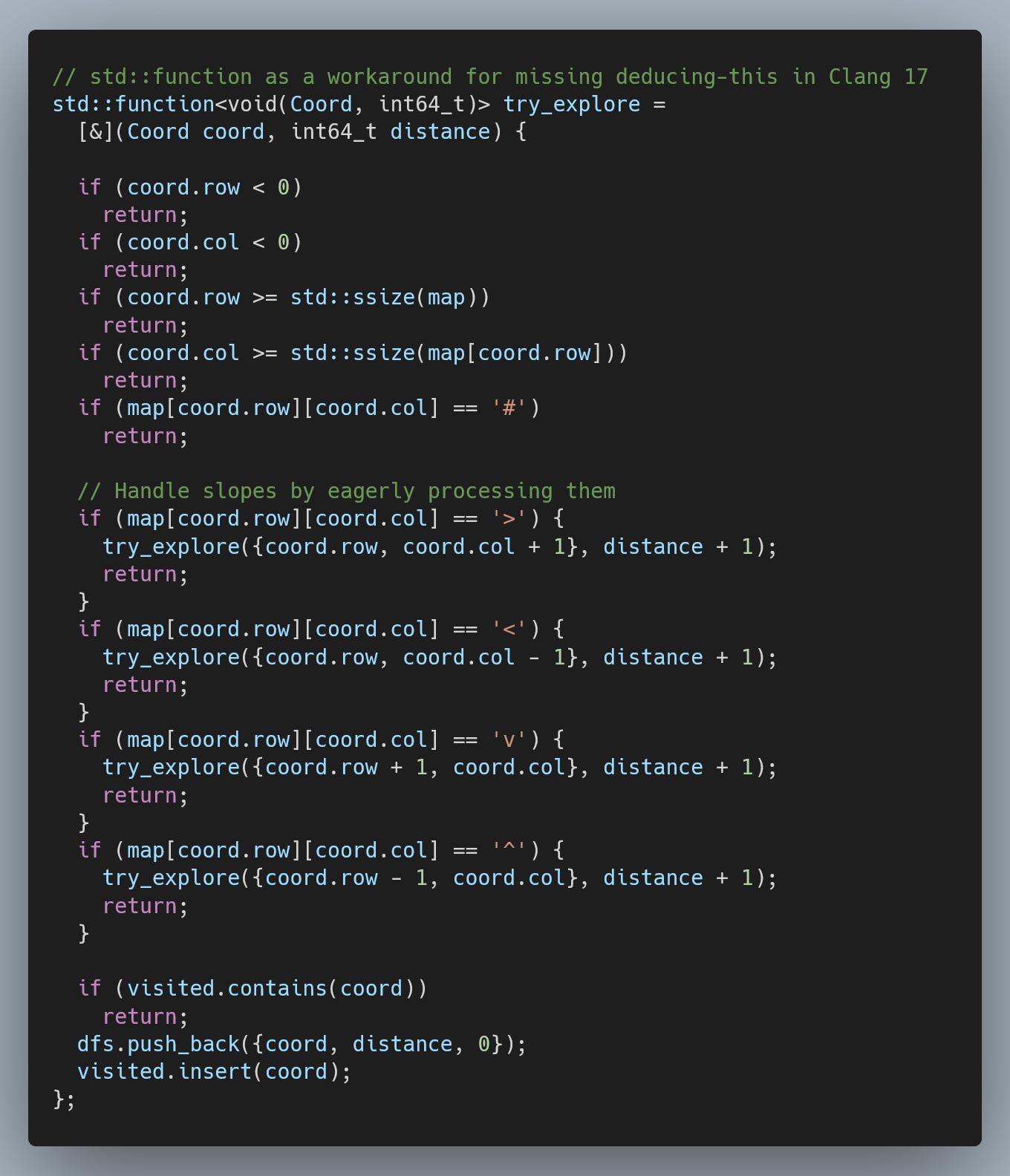
For part one, we are looking for the longest path. There are no real complications for now, and the input is easy to brute force using DFS. However, since the input is fairly large, I have at least opted for a non-recursive version.
The main complexity that comes from a non-recursive implementation of DFS is that we need to remember which direction we have already tried for each space. In a recursive version, this is implicitly encoded in the code.
As usual, I have wrapped the “step” function into a lambda to avoid code duplication.
With the step function implemented, we can implement the non-recursive DFS while keeping track of the longest path.
Part two
Unfortunately, our solution will not work for part two because removing the slopes significantly increases the number of paths. At the same time, finding the longest path is an NP-hard problem (Wikipedia), meaning that the idea of our approach is correct.
What we need to do is to improve the performance of our search.
One way to do that is to translate our text input to the corresponding weighted graph, which wouldn’t require us to traverse the input one space at a time.
To translate the input, we can use hybrid BFS that searches over crossroads and relies on a helper that implements eager exploration to reach the crossroads on the other side of a path. We will store the result as a neighbourhood map.
We will need helpers to check for steppable spaces, and a helper will generate them for a coordinate.
Next, we will need a helper that does the eager exploration steps and finds the other crossroads on the other side of a path.
We can now put this together to form our BFS conversion algorithm. We explore in every direction from each crossroad, recording information about crossroads and the lengths of paths between them.
Because the resulting graph has only a few nodes, we can now decrease the complexity of our longest path search and use a straightforward recursive version.
Conclusion
How did you do with today’s problems? Did you use a different approach to optimize the search?
Share your solutions and insights. Check out the repository with solutions and links to all articles: https://github.com/HappyCerberus/aoc-2023-cpp-solutions.