Daily bit(e) of C++ | Detecting loops in singly-linked list
Daily bit(e) of C++ #114, Common interview problem: Detecting loops in singly-linked list.
Today we will look at a common interview problem: Detecting loops in a singly-linked list.
Given a singly-linked list, determine whether it is malformed (contains a loop).
If it does, return a pointer to the first node on the loop (nullptr if it doesn't).
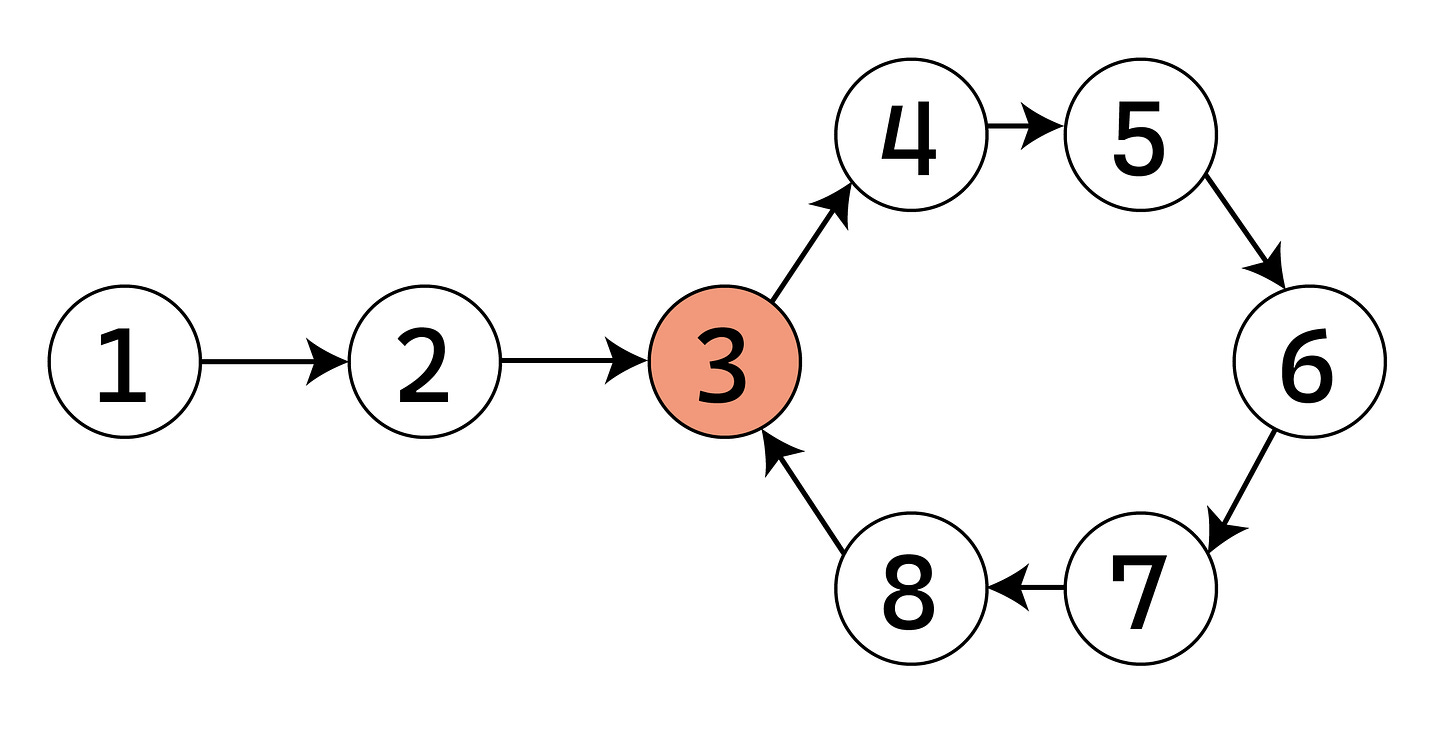
For example, in the above illustration, the start of the loop is the node containing value 3.
Before you continue reading the solution, I encourage you to try to solve it yourself. Here is a Compiler Explorer link with a couple of test cases: https://compiler-explorer.com/z/Mcd5PTjh4.
Solution
This problem is the prototypical problem for the fast and slow pointer technique (a.k.a. Floyd’s tortoise and hare).
We will eventually reach the end if we iterate over the list without a loop. However, if there is a loop, we will end up stuck in the loop.
If we use two pointers to iterate, one slow one, iterating normally and one fast one, iterating over two nodes in each step, we have a guarantee that if they get stuck in a loop, they will eventually meet.
That gives us a loop detection, but how do we determine which node starts the loop? For that, we must look at how many steps both pointers made when they met.
Consider that the slow pointer moved x steps before entering the loop and then y steps after entering the loop for a slow = x + y total.
The fast pointer moved similarly. It also moved x steps before entering the loop and then y steps after entering the loop when it met up with the slow pointer; however, before that, it did an unknown number of loops: fast = x + n*loop + y. Importantly, we also know that the fast pointer also did 2*slow steps.
If we put this together, we end up with the following:
2*(x+y) = x + n*loop + y
x = n*loop - y
This means that the number of steps to reach the loop is the same as the number of steps remaining from where the pointers met up to the start of the loop.
So to find it, we can iterate from the start and the meeting point. Once these two new pointers meet, we have our loop start.