Daily bit(e) of C++ | Largest covered interval
Daily bit(e) of C++ #296, Common interview problem: Largest covered interval.
Today, we will look at a common C++ interview problem: Largest covered interval.
Given an array of integers, return the size of the largest interval that is fully covered by the values in this array.
For example, for the input {5,97,2,4,12,96,3,98}, the largest covered interval is [2,5], size four.
Before you continue reading the solution, I encourage you to try to solve it yourself. Here is a Compiler Explorer link with a couple of test cases: https://compiler-explorer.com/z/ehh9M6nEs.
Solution
The straightforward solution to this problem would be to sort the array, after which we can quickly determine the largest interval by scanning the array. However, this approach has O(nlogn) complexity dictated by the sort.
As mentioned, the above solution has O(nlogn) complexity, so the question is whether we can improve it. However, keep reading because we will revisit the above solution at the end of the article.
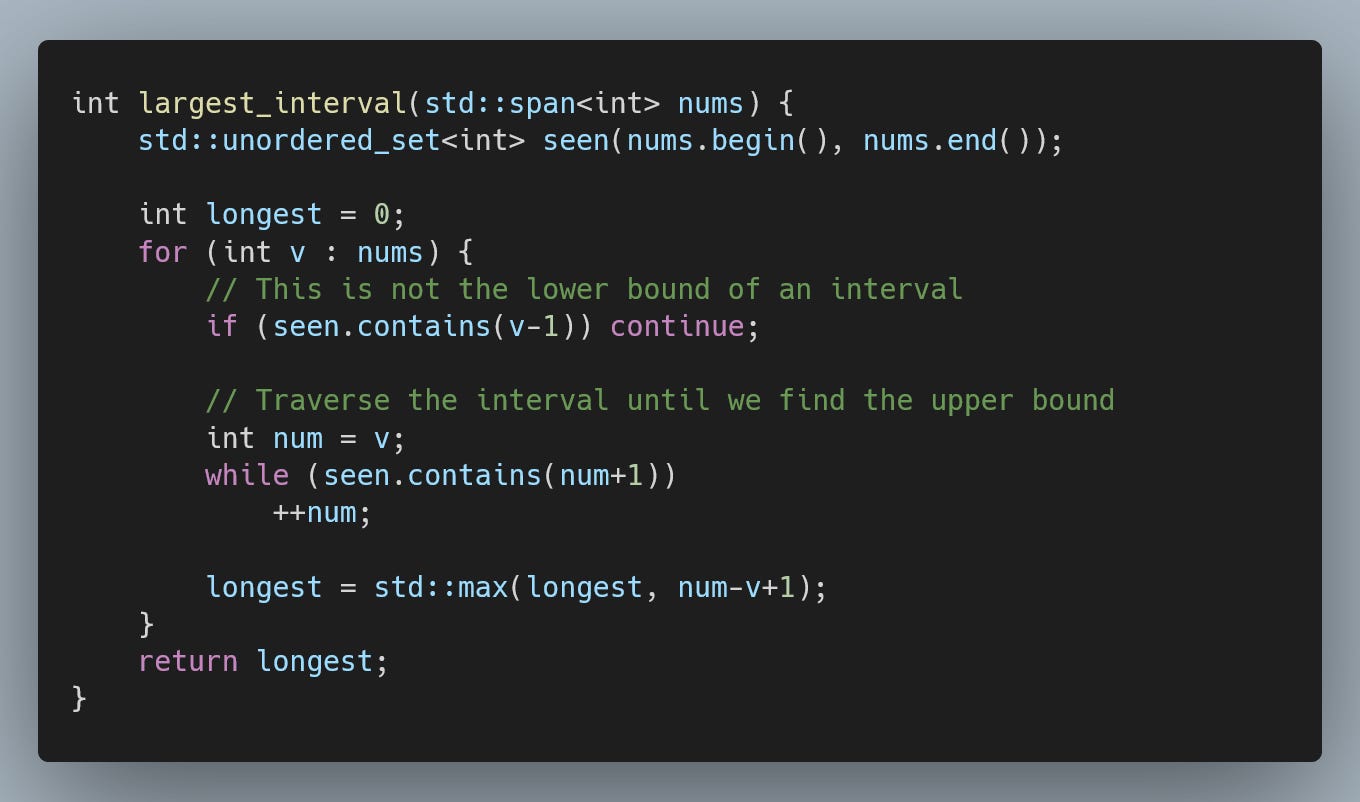
When we scan through the array, we rely on the sorted nature of the array to check the previous element for a match. However, we are only interested in the presence of said value anywhere in the array, and the sorting gives us locality.
Note that when we encounter a value v:
if v-1 is not in the array, this is the lower bound of an interval
if v+1 is not in the array, this is the upper bound of an interval
We store all elements in a std::unordered_set and then traverse the array. When we encounter the lower bound of an interval, we increment the value until we find the upper bound, giving us the length of this interval.
Because we traverse each interval only once, we end up with total O(n) complexity.
These two solutions are a perfect pair that demonstrates the difference between practical and theoretical complexity. Let’s consider what the logn means in practical terms.
We are working with 64-bit architecture, meaning logn will be at most 64. This gives us a reasonably strict requirement for O(1) operations (i.e. 64 cycles).
Whenever comparing an O(n) vs an O(nlogn) solution, it is critical to benchmark and understand the overhead of the O(n) solution. In this case, the sort-based solution will perform better even for 1M elements:
One interval, ordered:
Sort: 7441753ns
Set: 57615317ns
One interval, reverse order:
Sort: 7391188ns
Set: 53184698ns
Each element is an interval:
Sort: 10202918ns
Set: 53066629nsOpen the above benchmark in Compiler Explorer.