Daily bit(e) of C++ | Linked lists
Daily bit(e) of C++ #140, C++ linked lists in interview problems.
Today we will take a short departure from the typical interview content schedule, and instead of an interview problem, we will go over a bit of theory and talk about linked lists.
While rare in practical applications, linked lists crop up frequently in interviews. Partly this is because the node structure lends itself to formulating tricky problems, similar to trees and graphs, without the added topological complexity.
std::list and std::forward_list
The standard library offers two list types, std::list - a doubly-linked list and std::forward_list - a singly-linked list. Forward list exists primarily as a space optimization, saving 8 bytes per element on 64-bit architectures.
Both offer perfect iterator and reference stability, i.e. the only operation that invalidates iterators or references is the erasure of an element, and only for the removed element. The stability does extend even to moving elements between lists.
The iterator stability is one of the use cases where we would use a std::list or std::forward_list in practical applications. The only reasonable alternative would be wrapping each element in a std::unique_ptr, which does offer reference stability (but not iterator stability) irrespective of the wrapping container.
Of course, we do pay for this stability with performance. Linked lists are node-based containers, meaning each element is allocated in a separate node, potentially very distant from each other in memory. When we combine this with the inherent overhead of the indirection, traversing a std::list can regularly end up 5x-10x slower than an equivalent flat std::vector.
Aside from iterator stability, we also get access to a suite of O(1) operations, and these can potentially outweigh the inherent overhead of a std::list.
We are locked out of some standard algorithms because std::list only provides bidirectional iterators and std::forward_list only forward iterators. Both lists expose custom implementations of sort, unique, merge, reverse, remove and remove_if as member functions.
The std::forward_list has an additional quirk; since we can only erase and insert after an iterator, the std::forward_list offers a modified interface.
Custom lists
When implementing a simple custom linked list, you might be tempted to use a straightforward implementation using a std::unique_ptr.
Sadly, this approach isn't usable. The fundamental problem here is the design. We are mixing ownership with structural information. In this case, this problem manifests during destruction. Because we have tied the ownership with the structure, the destruction of a list will be recursive, potentially leading to stack exhaustion and a crash.
If we desire both the O(1) operations and iterator stability, the only option is to rely on manual resource management (at which point we might as well use std::list or std::forward_list).
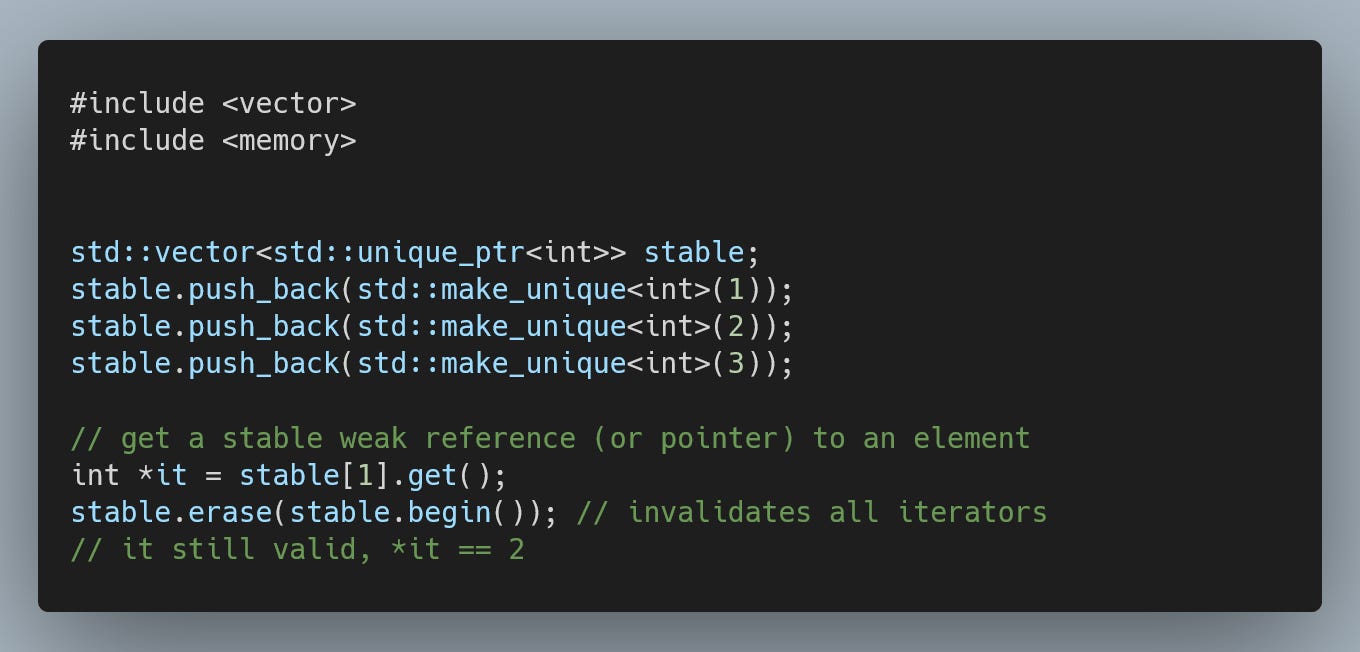
If we want to capture the structure of a linked list with reference stability, we can rely on the aforementioned std::vector and std::unique_ptr combination.
The crucial difference from the previous approach is that the list owns all nodes, and the structure is encoded only using weak pointers.
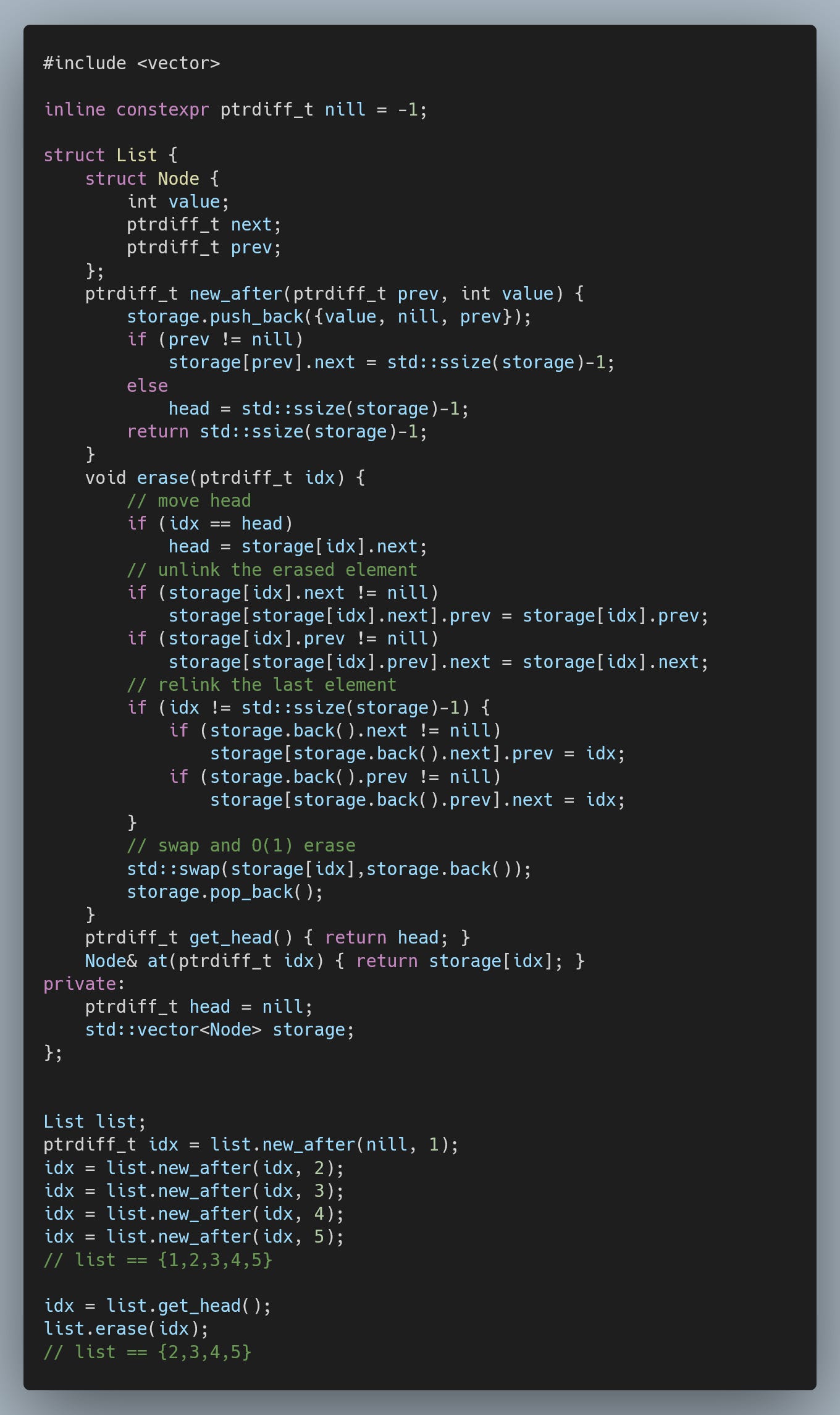
Finally, if we do not require stable iterators or references but do require O(1) operations, we can use a flat list approach. We can store all nodes directly in a std::vector. The only problematic operation, in that case, is erase(), which is inherently linear for std::vector.
However, a linked list already inherently encodes the order of elements, so instead of erasing from the middle of a std::vector, we can always erase from the end by swapping the to-be-erased element with the last element in the std::vector.
Basic operations
When designing a solution for a coding problem, the three most frequent operations with linked lists are:
merge two sorted lists
reverse a sorted list
scan with two iterators
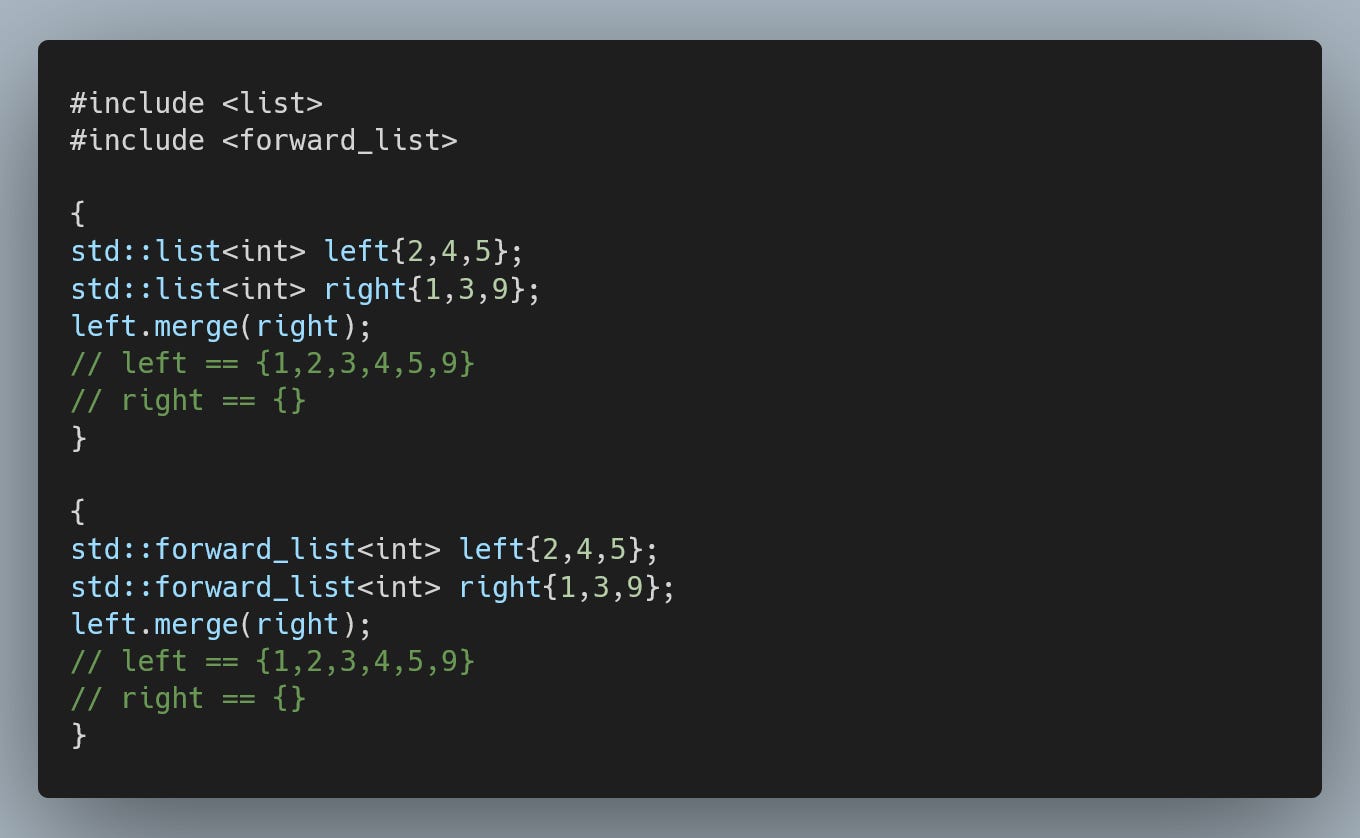
Both std::list and std::forward_list come with a built-in merge operation.
However, implementing one from scratch isn’t particularly complicated either. We consume the merged-in list, one element at a time, advancing the insertion position as needed.
The same situation applies to reversing a list. Both lists provide a built-in reverse operation with a custom implementation even simpler than merge.
Finally, scanning with two iterators is a common search technique for finding a sequence of elements that conform to a particular property. As long as this property is calculated strictly from elements entering and leaving the sequence, we do not need to access the elements currently in the sequence.












Good,thanks
very comprehensive. thanks.