Daily bit(e) of C++ | Longest increasing path
Daily bit(e) of C++ #30, Common interview problem: Longest increasing path
Today we will look at a common C++ interview problem: The longest increasing path.
Given a matrix where each element has an integer value, return the length of the longest increasing path, that is, a path where the value of each element is strictly larger than the previous elements in the path. Only orthogonally adjacent elements are considered neighbours (i.e. no diagonals).
In this example, the longest path is {1, 2, 4, 7, 8, 9}. Before you continue reading the solution, I encourage you to try to solve it yourself. Here is a link to Compiler Explorer with a couple of test cases: https://compiler-explorer.com/z/hPTMbPa1e.
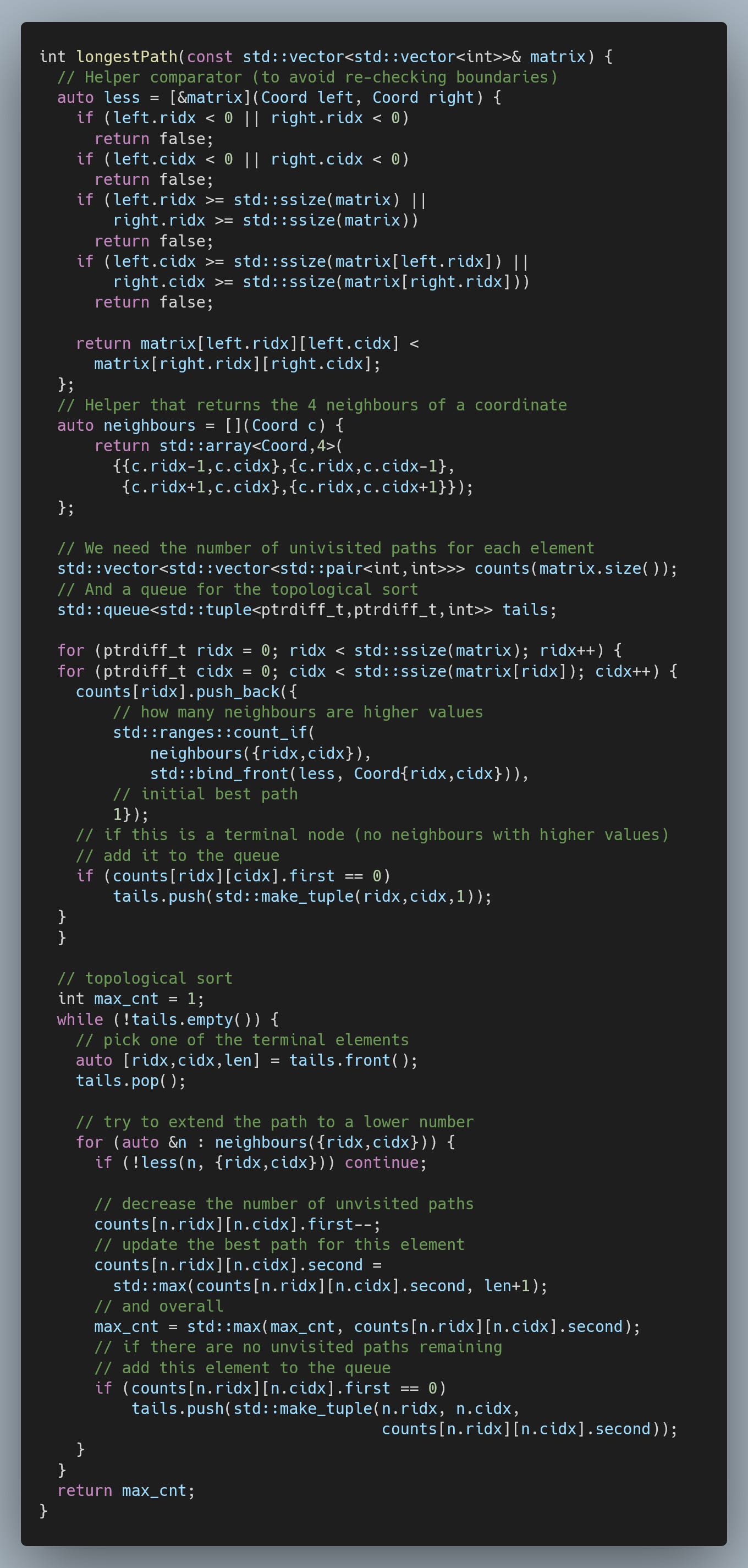
Solution
The first realization is that we do not have to care about loops, no matter what approach we choose. Since the paths are strictly increasing in value, they can never loop back.
This gives us the opportunity the use the idea of the topological sort. In our case, we can start from the nodes that have no outgoing paths (i.e. the ends of our paths), exploring the paths backwards while updating the number of outgoing paths for the neighbour nodes. Once a node reaches zero outgoing paths, it is now an end of the sub-path and is added to the queue of nodes to explore.
Finally, we need to keep track of the best sub-path as we do this exploration process.
The complexity of this solution is O(m*n), where m and n are the dimensions of the matrix. Each node is added to the queue once (once its outgoing number of paths reaches zero), and the maximum number of outgoing paths for each node is four (for the total number of decrements).