Daily bit(e) of C++ | Longest palindromic substring
Daily bit(e) of C++ #198, Common interview problem: Longest palindromic substring.
Today we will look at a common interview problem: Longest palindromic substring.
Given a string as a std::string_view, return the longest palindromic substring (if multiple, then the first one).
In the above example, the largest palindromic substring is “bab”.
Before you continue reading the solution, I encourage you to try to solve it yourself. Here is a Compiler Explorer link with a couple of test cases: https://compiler-explorer.com/z/fKT5MzoGE.
Solution
The brute-force solution (checking each substring for a palindrome) would take O(n^3). We can do better.
The first improvement is to take advantage of the inherent symmetry in palindromes. Palindromes expand from their centre, which we can mimic in our search. We expand from each potential centre until we encounter two characters that do not match. Keep in mind that the centre can be a character or the gap between two characters. We can end up doing O(n) comparisons for each centre, leading to O(n^2) overall complexity.
While the above approach is perfectly valid, we can save some trouble and a few characters by applying views and algorithms to the problem.
Either of the above approaches should be sufficient for an interview. However, there is an O(n) algorithm. Let’s think about the inefficiencies in our approach.
Let’s say we have just determined that the palindrome at the centre, signified by the white cell, has a radius of four (i.e. total length of 9), and the two red characters are different. Normally we would move on to the next centre, but we do have a lot of information we are not using. Because a palindrome is symmetric, we can re-use the information we have calculated for the previous centres.
If the largest palindrome at a previous centre is fully contained within our new palindrome, we can copy this information because the previous palindrome is part of the mirrored content.
If the largest palindrome at a previous centre expands beyond our current palindrome on the left, we have a slightly more complicated situation. We know that a portion of it is already mirrored. In this case, it is a palindrome with a radius of three. Can this palindrome still grow? Fortunately, it cannot. If it grew to size four, it would force the two red characters to be the same; however, that contradicts our preconditions.
Finally, let’s consider a palindrome that fits precisely into the boundary. This introduces the only case when the new palindrome can still grow because we cannot rule out that the orange cell matches the right red cell. However, we don’t have to start from scratch. We already know that the radius is at least three.
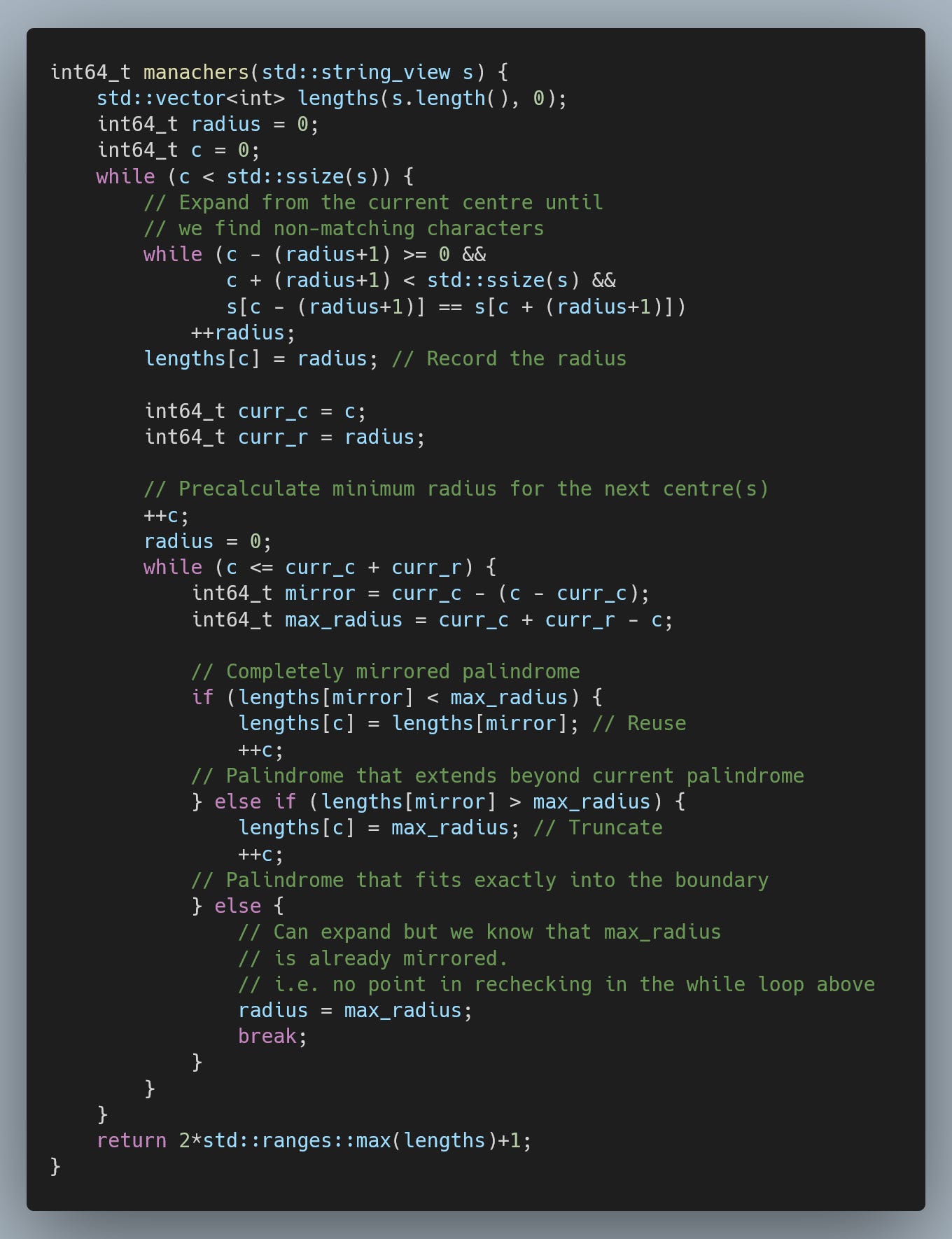
Putting the above observations, we end up with Manacher’s algorithm, which can find the largest palindromic substring in O(n). The following is a simplified version that only returns the size of the maximum palindrome.
However, you might have noticed that we assume we have a centre of a palindrome in character. This is the main downside of this algorithm, which can be alleviated by introducing dummy characters between each pair of characters. What would previously be an even-sized palindrome will now have a new centre in a dummy character.