Daily bit(e) of C++ | Maximum path in a tree
Daily bit(e) of C++ #21, Common interview questions: Maximum path in a tree
Today we look at the “Maximum path in a tree” interview problem.
Given a binary tree, where each node has an integer value, determine the maximum path in this tree.
A path is a sequence of nodes where every two consecutive nodes have a parent/child relationship, and each node is visited at most once. The value of a path is then simply the total of all the node values visited.
For this example, the maximum path has a value of nine (2+3+4).
Before you continue reading the solution, try to solve it yourself. Here is a Compiler Explorer link with a couple of test cases: https://compiler-explorer.com/z/hhYW4G3c4.
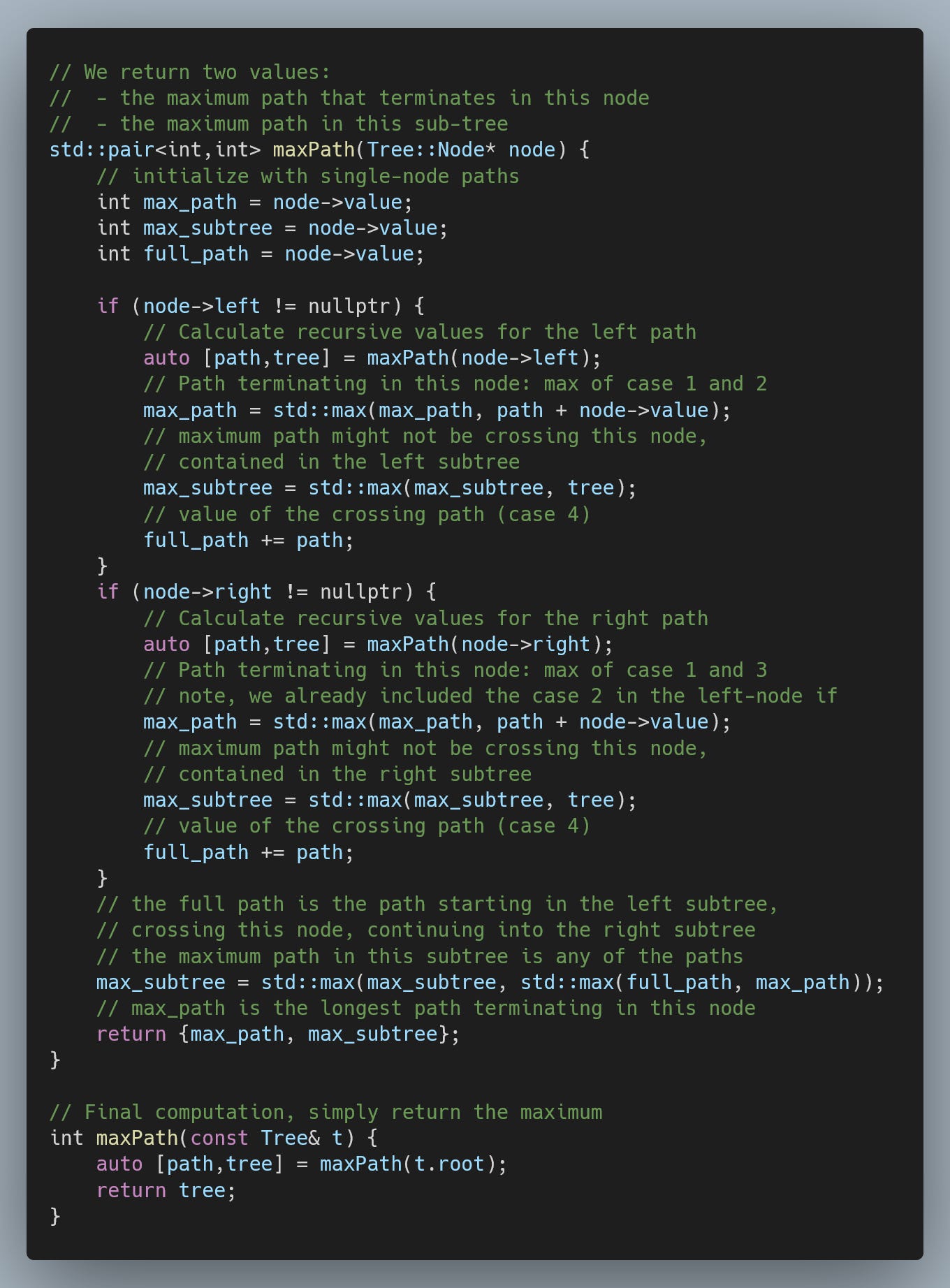
Solution
A typical trick with path-oriented problems is to consider a node that is part of the path. In this case, let's consider a root of a subtree.
Only four possible paths can be the maximum path crossing this node:
a single-node path that contains this node only
a path coming from the left child, terminating in this node
a path coming from the right child, terminating in this node
a path crossing this node, i.e. going from one child, crossing this node, continuing to the other child
These values are trivially computable as long as we know the maximum paths that terminate in the left and right child. And by computing 2. and 3., we calculate the maximum path that terminates in this node.
Finally, the maximum path in a tree crosses the root node (in which case, we already know how to calculate it) or is fully contained in one of the two child sub-trees. To calculate the maximum path in a sub-tree, we can apply the same logic recursively.