Daily bit(e) of C++ | Minimize deviation in an array
Daily bit(e) of C++ #177, Common interview problem: Minimize deviation in an array.
Today we will look at a common C++ interview problem: Minimize deviation in an array.
Given an array of unsigned integers, determine the minimum deviation achievable by repeatedly applying the following operations:
divide an even element by two
multiply an odd element by two
The deviation of an array is the difference between the maximum and minimum elements.
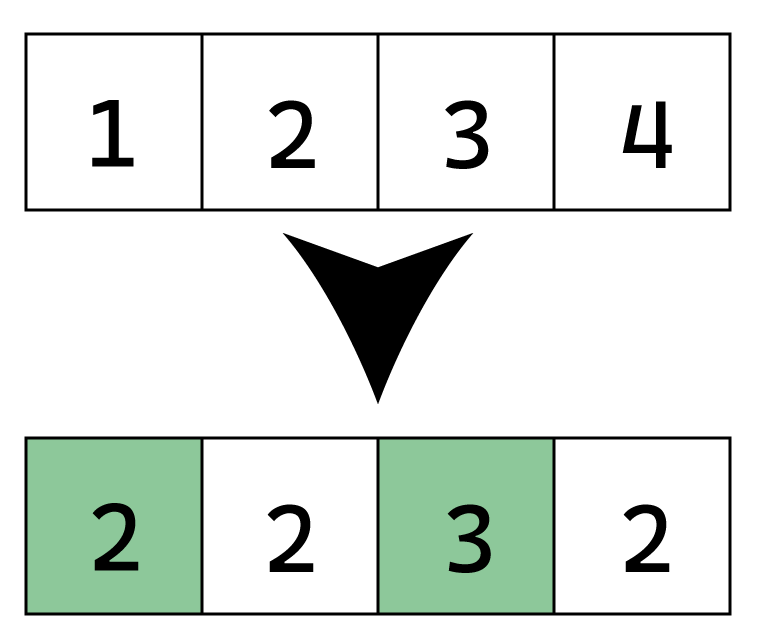
For example, for the array {1,2,3,4}, the minimum deviation is one, which is achieved by multiplying the first element by two and dividing the last element by two.
Before you continue reading the solution, I encourage you to try to solve it yourself. Here is a Compiler Explorer link with a couple of test cases: https://compiler-explorer.com/z/n6654cMEj.
Solution
First, let’s consider the operations we can apply. If an element starts odd, the only two values we can reach are {value, value*2}. If an element starts even, we can divide it by two until we reach an odd number {value, value/2, value/4, …}.
Instead of an array of integers, we have an array of sorted sequences of integers, and our goal is to find the smallest interval that covers each of the sequences.
If you are following this series, this will sound very familiar. And, yes, this is the “Smallest interval covering k sorted sequences” problem from Daily bit(e) #147:
Because the content of the sequences is so well-behaved (each element is 2x the previous), we can store the sequences implicitly using the minimum and maximum values.
Then we follow the approach from the “Smallest interval covering k sorted sequences”. We start considering the minimum values of each of the sequences. Because the only operation that could improve the current formed interval is removing the element that is the current low bound of the interval and replacing it with the next element from the same sequence, we repeat this process, iterating until we have no more elements to pick.
This solution also has interesting complexity. Consider N the number of elements in the original array and M the largest value in the original array. The largest potential sequence our operations generate is log(M). Since we iterate until we run out of elements in one of the sequences, we will iterate over N*log(M) elements. Inside our loop, we have one log(N) insertion operation, leading to a total complexity of N*log(M)*log(N).