Daily bit(e) of C++ | N-Queens
Daily bit(e) of C++ #58, The common interview problem: N-Queens
Given the number of queens, solve the N-queen problem.
I.e. produce all possible placements of queens where no queens are attacking each other (each queen is on a unique column, row, and diagonals).
Output the result as a vector of solutions, where each solution is a vector of the column positions of the queens.
For example, for the above, the output would be: {{1,3,0,2}, {2,0,3,1}}.
Before you continue reading the solution, I encourage you to try solving it yourself. Here is a compiler explorer link with a couple of test cases: https://compiler-explorer.com/z/EvK7hEsf4.
Solution
From the big-O perspective, there isn’t much we can do. We need to iterate over all possible solutions, and if we do it in an ordered manner, we end up with O(n!) (the first queen has n available column positions, the second has n-1, and so on).
The problem, therefore, turns into the problem of doing this efficiently. Checking whether a column is occupied is easily done with a vector of booleans. To do the same with diagonals, we need to make an observation.
If we take the difference between the row and column index, the diagonals will end up with the same values; therefore, we can index using this value and again easily keep track of the occupied diagonals. And we can use a very similar logic for orthogonal diagonals, this time using the sum of the row and column.
We can wrap this logic into a helper, from which we will need the check (whether a row and column combination is still feasible) and two methods to (un)mark a given row and column combination as occupied.
The rest of the problem is a straightforward depth-first search/backtracking algorithm.
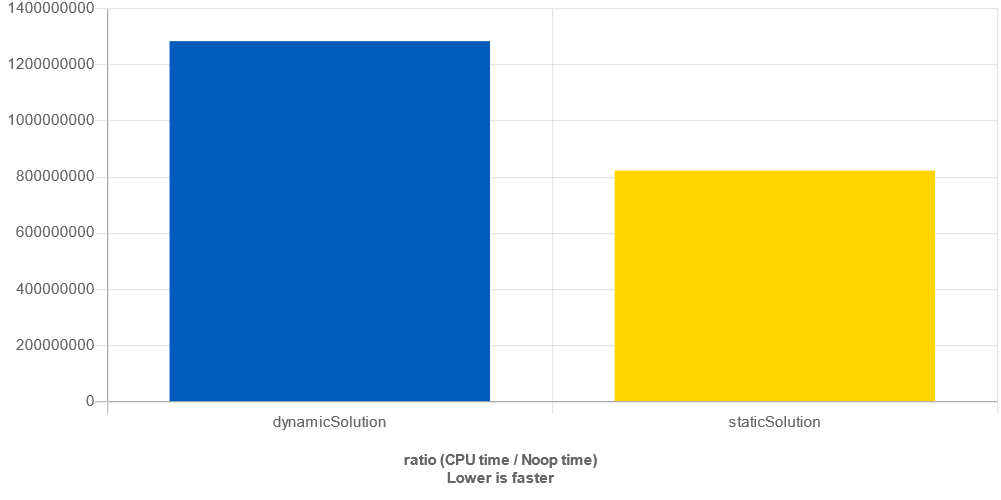
This problem is also a good opportunity to explore the difference between dynamic and static approaches. In our solution, we take the size of the problem as a function argument. If we switch the size to a compile-time constant, we can gain a non-trivial amount of performance.
We can keep our DFS part of the solution the same but switch the State to a static one using std::array and std::bitset.
This simple change is responsible for ~1.5x speedup.