Daily bit(e) of C++ | Number of reorders of a serialized BST
Daily bit(e) of C++ #212, Common interview problem: Number of reorders of a serialized BST.
Today we will look at a common C++ interview problem: Number of reorders of a serialized BST.
Given a permutation of 1..N as std::vector<int>, return the number of other permutations that produce the same BST. The BST is produced by inserting elements in the order of their indexes (i.e. left-to-right).
Because the number of permutations can be high, return the result as modulo 10^9+7.
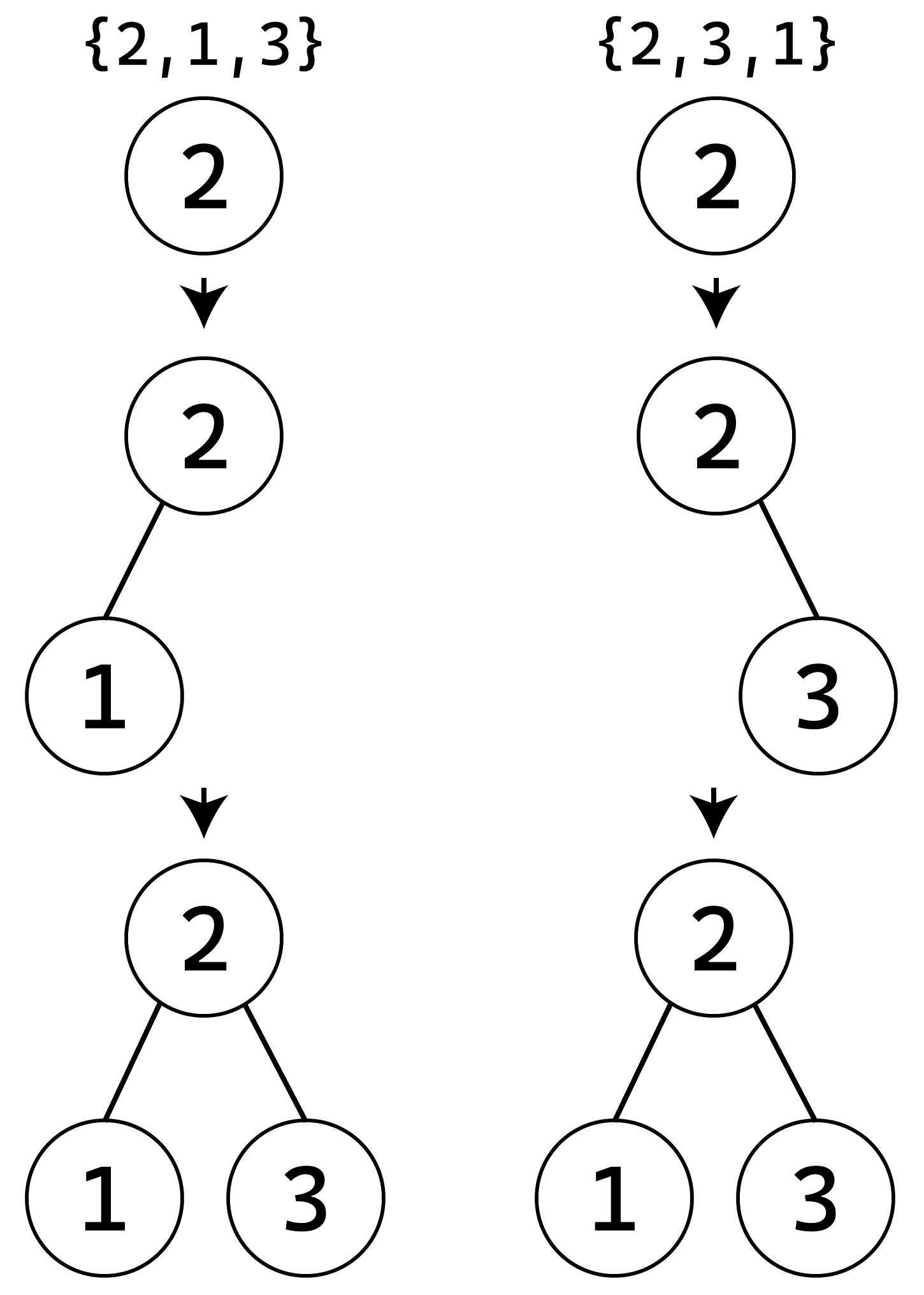
For example, for the permutation {2,1,3}, there is one other permutation that produces the same BST: {2,3,1}.
Before you continue reading the solution, I encourage you to try to solve it yourself. Here is a Compiler Explorer link with a couple of test cases: https://compiler-explorer.com/z/aPjrnoafP.
Solution
First, let’s remind ourselves how Binary Search trees operate. For each node, all the nodes in the left subtree are lower than the value of this node, and all nodes in the right subtree are higher than the value of this node.
This allows us to find any node with a specific value in log(n).
Determining the number of reorderings that produce the same BST is much less obvious. However, the first fairly straightforward observation is that the first node will always be the root node, and it creates a partition over the other nodes (for the left and right subtrees).
This points to the first part contributing to the total count of reorderings. Any reordering of elements that produces the same stable partition will lead to the same BST.
Let’s consider the permutation {3,1,2,4,5}. Changing the order of elements within each partition (i.e. {1,2}, {4,5}) would produce different partitions; however, we can freely interleave these partitions without changing the result. More formally, we are looking for the number of ways to pick the positions for the left (or right) partition out of all positions, i.e. C(n-1,k) (binomial coefficient), where n is the total number of elements in the permutation and k is the number of elements in the left partition.
The second point we have not considered is the number of reorderings in the two sub-tree, which we can calculate recursively.
This leads to a total formula: reorderings(left)*reorderings(right)*coeff(n-1,left.size()).
This implies that we will have to pre-calculate the binomial coefficients, which we can do using Pascal’s triangle.
Finally, we need to apply the requested modulo operation where appropriate.