Daily bit(e) of C++ | Tree traversal algorithms
Daily bit(e) of C++ #18, The algorithms worth knowing: tree traversal
While the C++ standard library offers a wide range of algorithms, one type that is sadly completely missing so far is graph (and consequently tree) algorithms. While this is being worked on (see P1709), the only choice, for now, is to reproduce the standard solutions from scratch when graph algorithms come up in coding interviews.
Introduction
Before we start with the tree traversal algorithms, it’s worth talking about the tree data structure.
The most straightforward approach to represent a tree is using a single struct:
This approach is straightforward and offers a convenient interface. For example, splicing the tree only requires calling std::swap on the source and destination std::unique_ptr.
However, it suffers a fatal flaw. Because our data structure is recursive, and we rely on generated destructors, we end up with recursive destruction. A deep enough tree can quickly exhaust the stack during its destruction, leading to memory corruption or a crash.
We can mitigate this problem by separating the representation of the tree structure from the memory management:
This completely removes the recursive destruction; however, we pay for that. While we can still splice easily within a tree, splicing between trees becomes cumbersome.
Since we are talking about C++, it’s worth mentioning that neither of the above approaches is performance-friendly. The biggest problem is that we are allocating each node separately, which means that they can be allocated far apart, in the worst case, each node mapping to a different cache line.
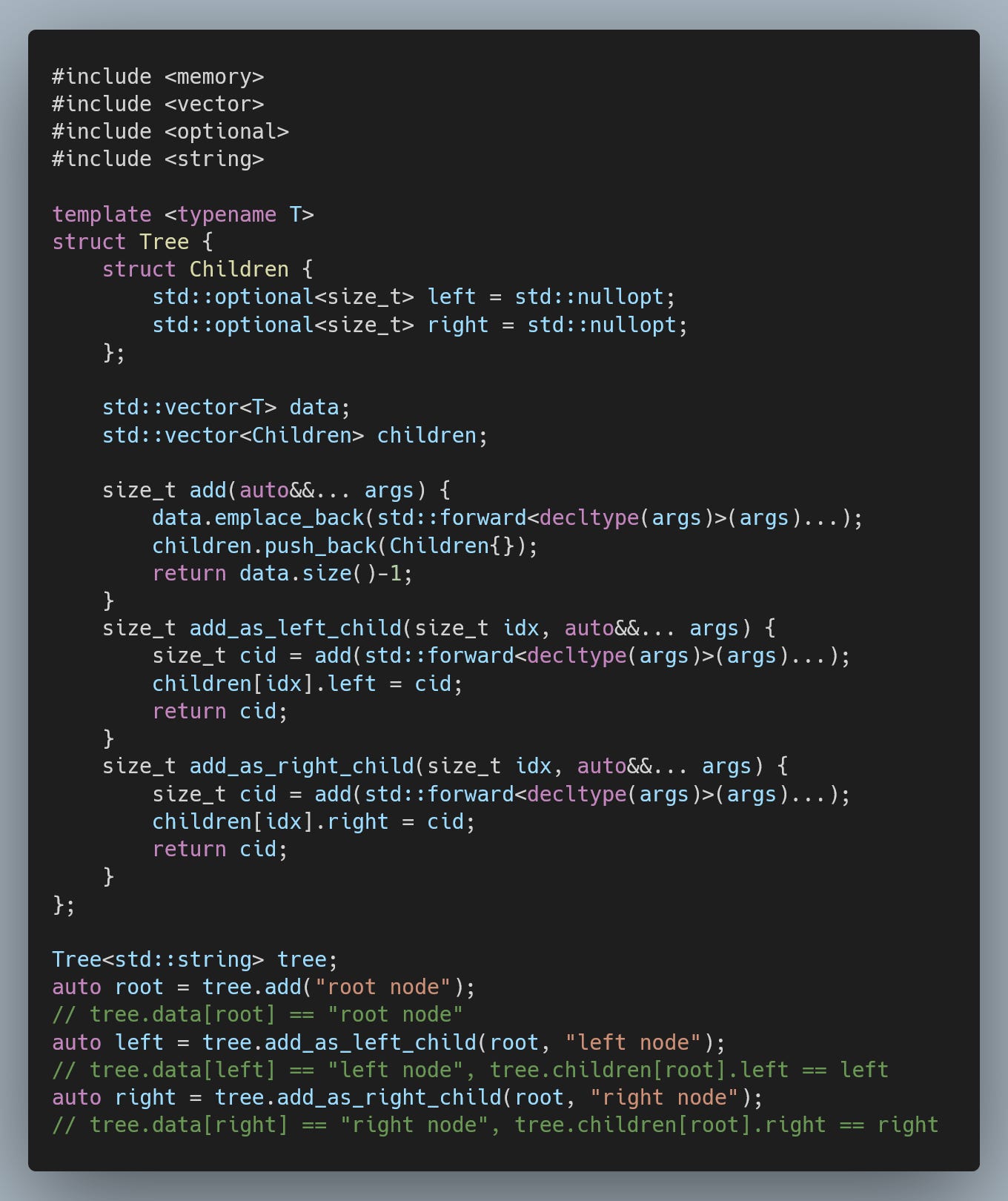
One way to address this problem is to store the nodes inline, with the information about which node is whose child stored separately:
Note that we are again adding complexity. This is because we no longer have stable addresses, and each node addition can invalidate the locations of the previous nodes (due to how std::vector handles memory). We, therefore, need to rely on indices, which on the other hand, makes serialization trivial, as indices remain stable.
Tree traversals
There are four tree traversal types that are worth remembering as they regularly come up as part of coding interviews. We will review each of them and look at some typical applications.
Pre-order traversal
In pre-order traversal, each node is visited before its children.
Because of this ordering, pre-order traversal is commonly used for serializing and de-serializing.
As mentioned before, the recursive approach can be problematic due to stack exhaustion. So let’s also look at an alternative implementation using a std::stack.
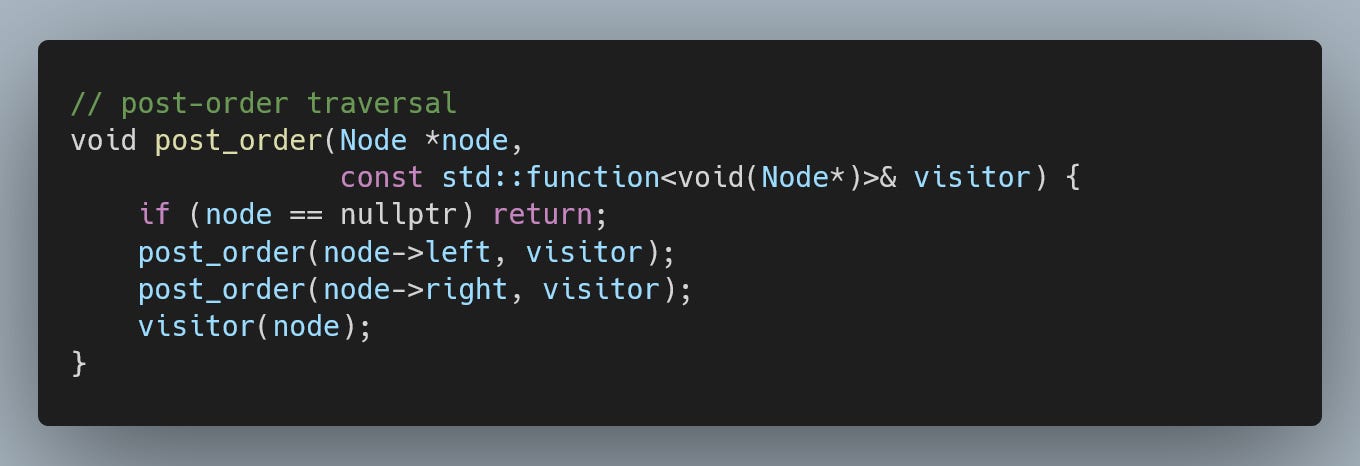
Post-order traversal
In post-order traversal, each node is visited after its children.
Because of this ordering, post-order can be used in expression trees, where we can only evaluate the parent expression if both its children were already evaluated.
For a non-recursive approach, we could visit all nodes in pre-order, remembering each (for example, using a std::stack again) and then iterate over the nodes in reverse order. However, we can do better:
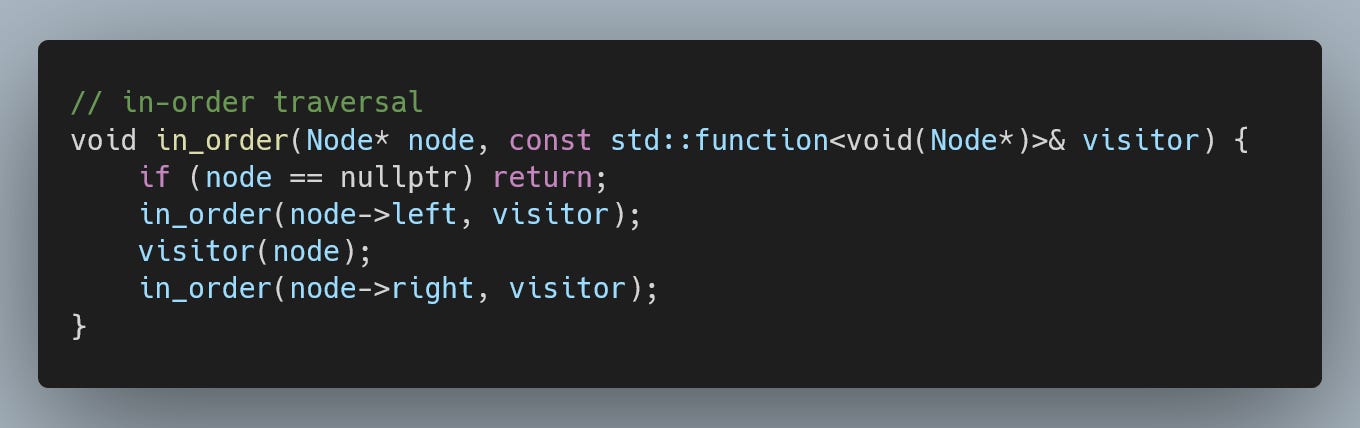
In-order traversal
In in-order traversal, we visit each node in between visiting its left and right children.
The typical use case is when traversing trees with some order to them, and we want that order to be maintained in the traversal.
For example, in the following example, we create a simple sorted binary tree (for each node, all the nodes in the left subtree have lower or equal values, and all the nodes in the right subtree have higher values) and then traverse it in-order to produce a sorted list of numbers:
The non-recursive approach is similar to post-order, but we remove the complexity of remembering the right child.
Rank-order traversal
Finally, it’s worth mentioning the rank-order or the level-order traversal, where we traverse the nodes in the order of their distance from the root node (and typically left-to-right).
While all the previous traversals were depth-first search based, this one is based on the breadth-first search algorithm.
Rank-order traversal typically comes up as part of more complex problems. By default, it can be used to find the closest node to the root that satisfies particular criteria or calculate the nodes' distances from the root.
Here is an example of calculating the maximum value at each level of a tree:
Complexity
All the algorithms I talked about are traversals, so they inherently have O(n) time complexity. However, it’s worth mentioning the space complexity.
For the depth-first based traversals (pre-order, post-order, in-order), the space complexity is dictated by the maximum depth in the tree.
For the breadth-first rank-order traversal, the space complexity is dictated by the maximum width in the tree.













Never thought,that traversal can be differs from 1st variant ( parent, child, child). Great article. It is very helpful.
Excellent article, Simon, very thorough and helpful. Thanks!