Daily bit(e) of C++ | Uncovered intervals
Daily bit(e) of C++ #37, The common C++ interview problem: Uncovered intervals
Today we will look at a common C++ interview problem: Uncovered intervals.
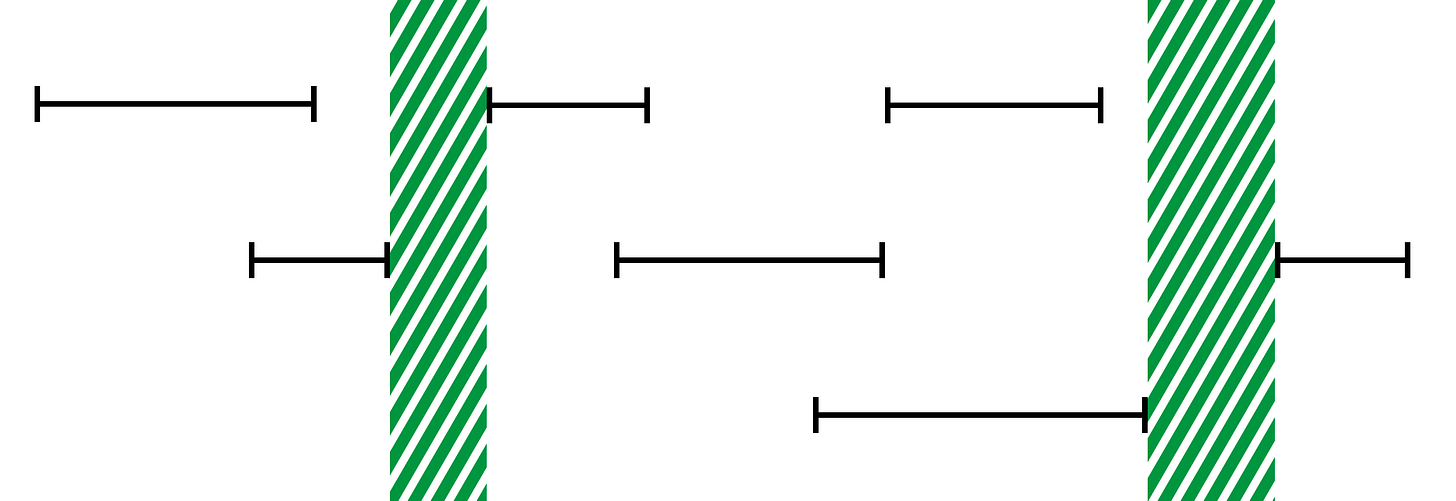
Given a list of schedules, where each schedule is a sorted sequence of non-overlapping intervals, return the list of finite (i.e. ignore the infinite before and after) intervals that are not covered by any of the intervals.
The intervals are half-open, i.e. an interval {10, 15} covers 10, 11, 12, 13 and 14 (not 15).
As an additional (C++ specific) challenge, avoid unnecessary copies of the input data.
Before you continue reading the solution, try to solve it yourself. Here is a Compiler Explorer link with a couple of test cases: https://compiler-explorer.com/z/3zj4M4hW7.
Solution
We are already getting each schedule sorted and non-overlapping, making things much easier.
So when do we have an uncovered interval? If we process the intervals in the order of their start time and keep track of the latest end, we have an uncovered interval if the current start time is larger than the latest end. The gap is then simply {latest end, current start}.
Using a priority queue, we can pick the interval with the lowest start time in log(K) where K is the number of schedules. However, there is a problem. A priority queue doesn't allow for efficient element extraction; therefore, we would incur data copies. There are several ways around this problem. Here we use the heap algorithms, which work exactly like a priority queue, but on top of any random access container.
There is one final problem. As we process each schedule, we need to remove elements from the front of the schedule (as we move past that interval). Unfortunately, this is an O(n) operation for std::vector, so we need a workaround. Instead of working with the input directly, we can wrap each schedule into a std::span. The std::span is a lightweight view-style wrapper for contiguous data with a cheap creation of a sub-view that doesn't contain the first element.